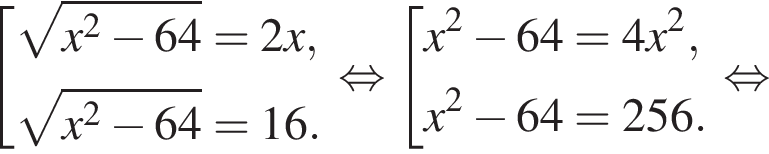
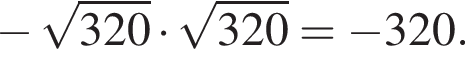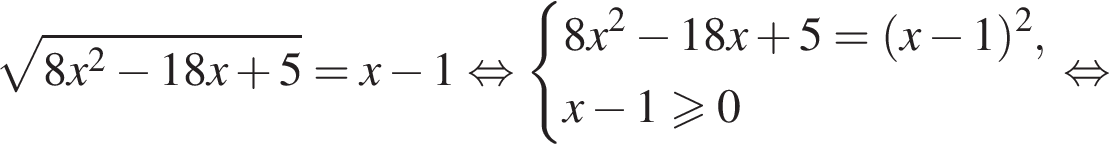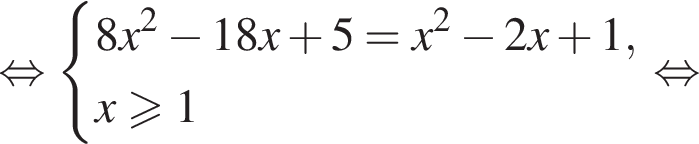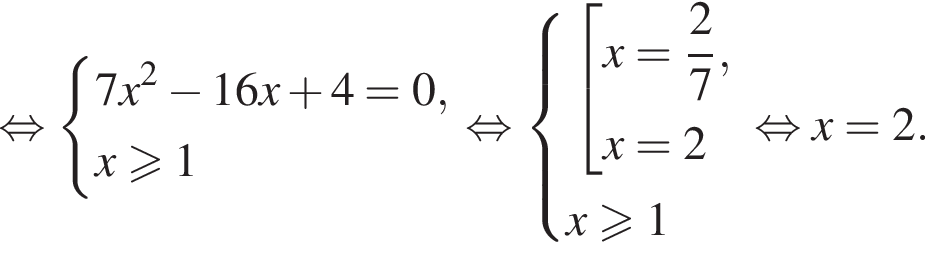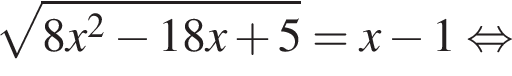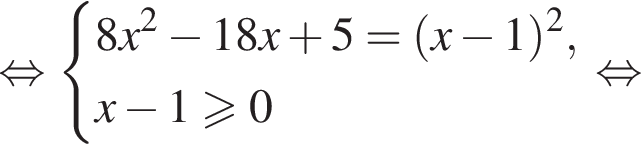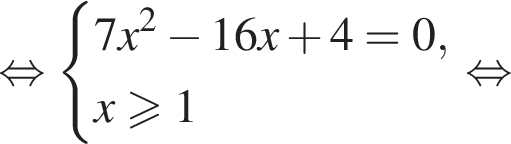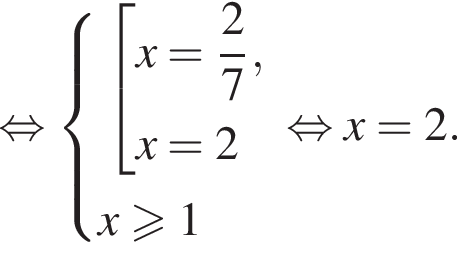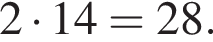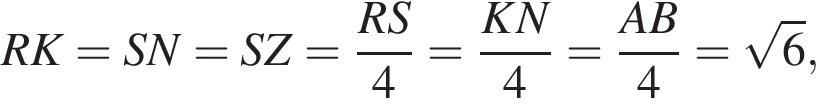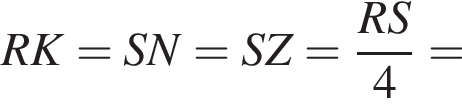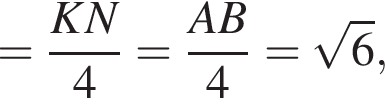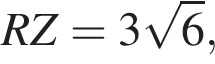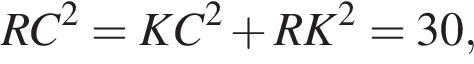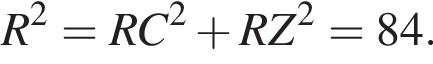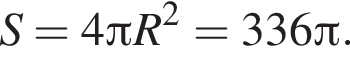Площадь круга равна ![]() Диаметр этого круга равен:
Диаметр этого круга равен:
Если 18% некоторого числа равны 24, то 30% этого числа равны:
Укажите верное равенство:
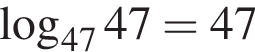
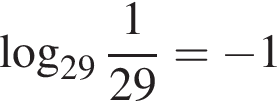
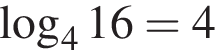
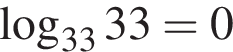
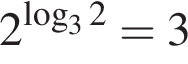
Сумма наибольшего и наименьшего значений функции
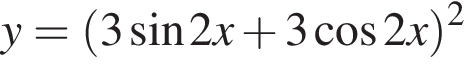
равна:
На координатной прямой отмечены точки А, В, С, D, E. Если расстояние между A и С равно ![]() то ближе других к точке с координатой 0,5 расположена точка:
то ближе других к точке с координатой 0,5 расположена точка:
Прямая a, параллельная плоскости α, находится от нее на расстоянии 2. Через прямую a проведена плоскость β, пересекающая плоскость α по прямой b и образующая с ней угол 60°. Найдите площадь четырехугольника ABCD, если A и B — такие точки прямой a, что AB = 5, а C и D — такие точки прямой b, что CD = 3.
Упростите выражение 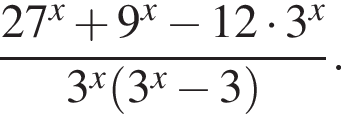
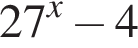
Сократите дробь 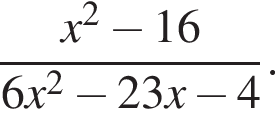
Среди значений аргумента x, равных ![]()
![]()
![]()
![]()
![]() укажите то, при котором значение функции
укажите то, при котором значение функции  меньше
меньше ![]()
Укажите номера верных неравенств, если известно, что 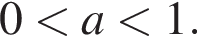

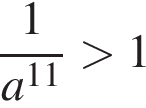
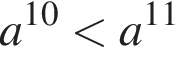
Витя купил в магазине некоторое количество тетрадей, заплатив за них 24 тысячи рублей. Затем он обнаружил, что в другом магазине тетрадь стоит на 1 тысячу рублей меньше, поэтому, заплатив такую же сумму, он мог бы купить на 2 тетради больше. Сколько тетрадей купил Витя?
В равнобедренную трапецию, площадь которой равна ![]() вписана окружность. Сумма двух углов трапеции равна 60°. Найдите периметр трапеции.
вписана окружность. Сумма двух углов трапеции равна 60°. Найдите периметр трапеции.
Найдите сумму целых решений неравенства 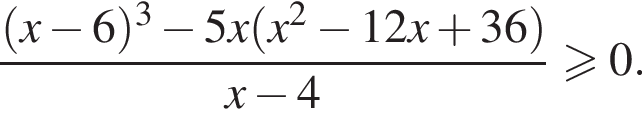
Внешний угол правильного многоугольника равен 45°. Выберите все верные утверждения для данного многоугольника.
1. Многоугольник является восьмиугольником.
2. Сумма всех внутренних углов составляет 1080°.
3. Если сторона многоугольника равна 2, то радиус вписанной окружности равен 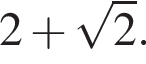
4. Площадь многоугольника можно вычислить по формуле  где R — радиус описанной окружности.
где R — радиус описанной окружности.
Ответ запишите в виде последовательности цифр в порядке возрастания. Например: 123.
Найдите сумму наименьшего и наибольшего целых решений неравенства 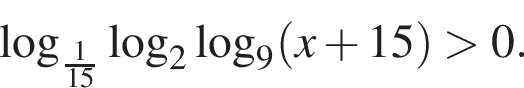
Решите уравнение 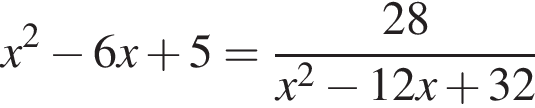 и найдите сумму его корней.
и найдите сумму его корней.
Площадь прямоугольника ABCD равна 35. Точки M, N, P, Q — середины его сторон. Найдите площадь четырехугольника между прямыми AN, BP, CQ, DM.
Найдите значение выражения 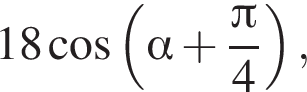 если
если 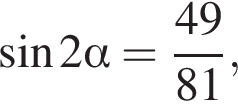
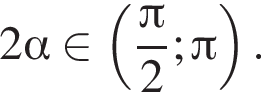
Найдите наибольшее целое решение неравенства 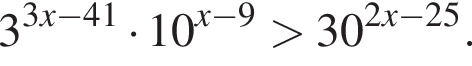
Выберите три верных утверждения:
1) если 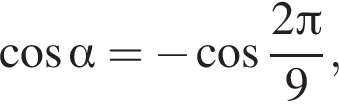 то
то 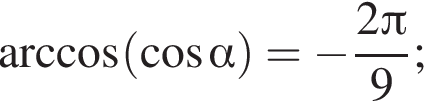
2) если 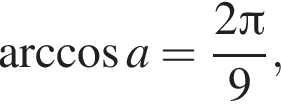 то
то 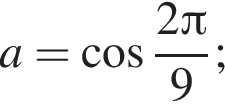
3) если 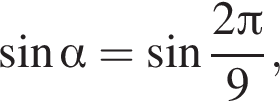 то
то 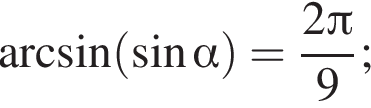
4) если 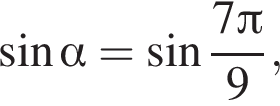 то
то 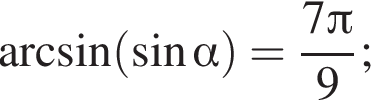
5) если 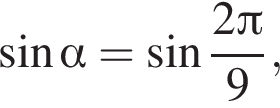 то
то 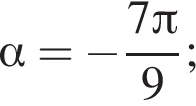
6) если 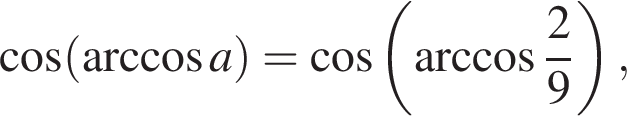 то
то 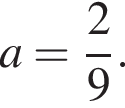
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
В арифметической прогрессии 130 членов, их сумма равна 130, а сумма членов с четными номерами на 130 больше суммы членов с нечетными номерами. Найдите сотый член этой прогрессии.
На рисунке изображены графики движения пяти мотоциклистов. Для начала каждого из предложений A−B подберите его окончание 1−5 так, чтобы получилось верное утверждение.
A) График движения мотоциклиста, который двигался с наибольшей скоростью, обозначен буквой ...
Б) График движения-мотоциклиста, который двигался с наименышей скоростью, обозначен буквой ...
В) График движения мотоциклиста, который двигался со скоростью 44 км/ч, обозначен буквой ...
1) A
2) B
3) C
4) D
5) F
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Верхнюю сторону листа фанеры прямоугольной формы разделили для покраски прямой линией на две части так, как показано на рисунке. Треугольную часть (I) покрасили краской белого цвета, а четырехугольную (II) — краской серого цвета. Сколько серой краски (в граммах) было использовано, если краски белого цвета понадобилось 280 г и расход краски (г/см2) обоих цветов одинаков?
На рисунке изображен график функции
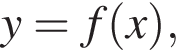 заданной на промежутке
заданной на промежутке 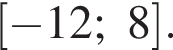 Найдите произведение значений аргумента, при которых
Найдите произведение значений аргумента, при которых 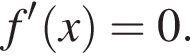 (Черными точками отмечены узлы сетки, через которые проходит график функции
(Черными точками отмечены узлы сетки, через которые проходит график функции 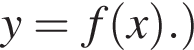
Пусть (x1; y1), (x2; y2) — решения системы уравнений 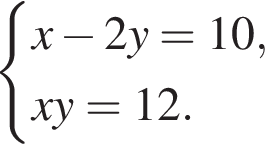 Найдите значение выражения
Найдите значение выражения 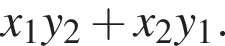
В остроугольном треугольнике ABC проведены высоты BE и CD. Найдите длину CB, если 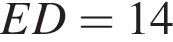 и радиус окружности, описанной вокруг AED равен 25. Укажите в ответе величину 12CB.
и радиус окружности, описанной вокруг AED равен 25. Укажите в ответе величину 12CB.
Найдите сумму всех целых чисел из области определения функции 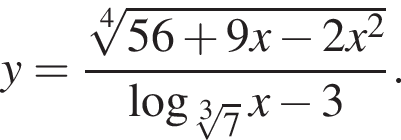
Найдите произведение корней уравнения 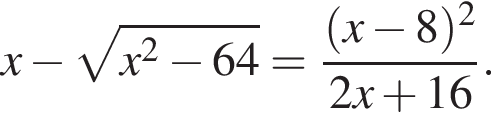
Найдите сумму корней (корень, если он единственный) уравнения 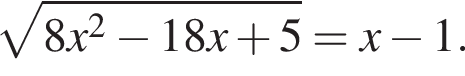 В ответ запишите полученный результат, увеличенный в 14 раз.
В ответ запишите полученный результат, увеличенный в 14 раз.
ABCDA1B1C1D1 — куб, длина ребра которого равна ![]() Сфера проходит через его вершины В и D1 и середины ребер BB1 и CC1. Найдите площадь сферы S, в ответ запишите значение выражения
Сфера проходит через его вершины В и D1 и середины ребер BB1 и CC1. Найдите площадь сферы S, в ответ запишите значение выражения ![]()

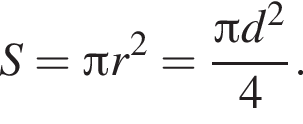 Следовательно,
Следовательно, 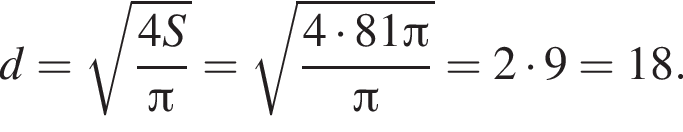
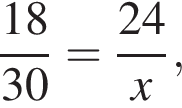 где x — неизвестное число.
где x — неизвестное число.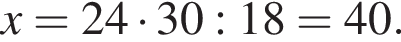
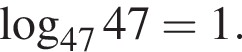
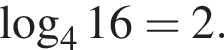
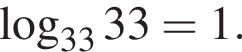
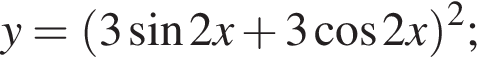
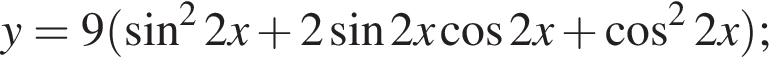

 имеем:
имеем:
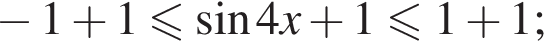
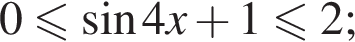
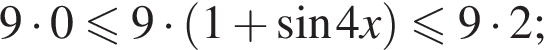
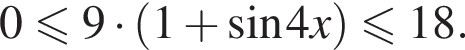
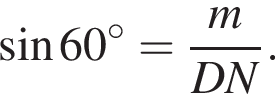
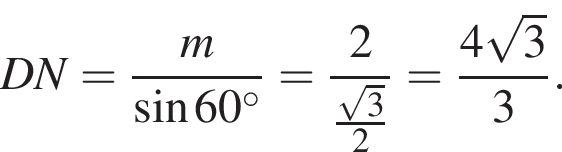
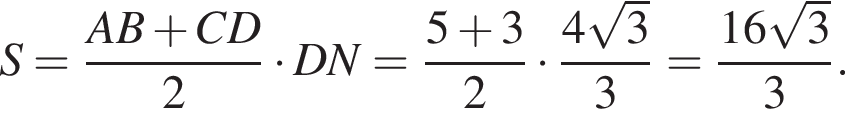
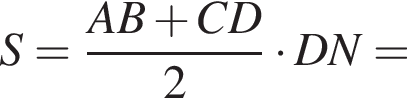
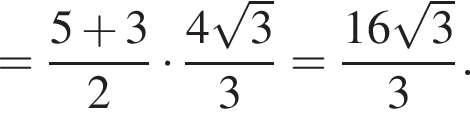
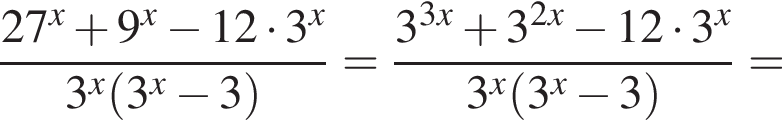
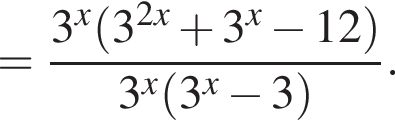
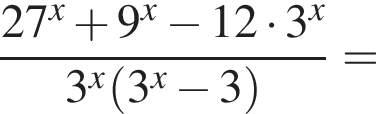
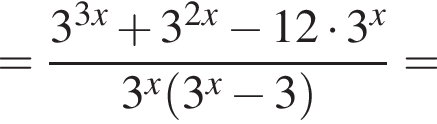
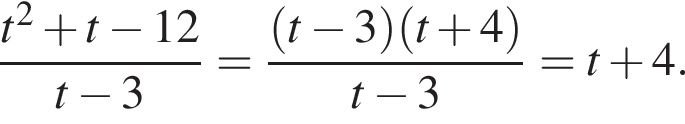 Тем самым, исходное выражение равно
Тем самым, исходное выражение равно 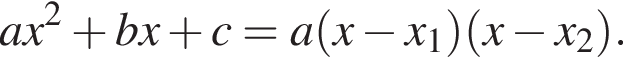
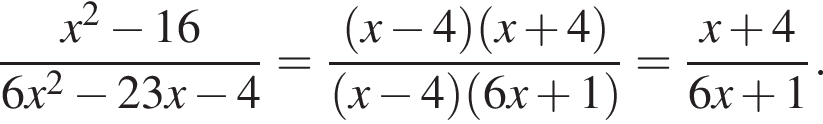
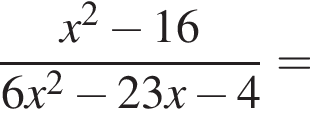
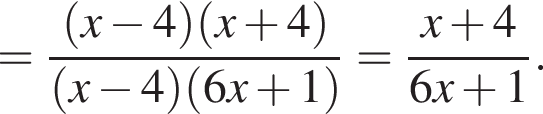
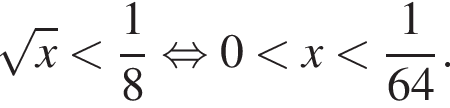 Среди значений аргумента x полученному неравенству удовлетворяет значение
Среди значений аргумента x полученному неравенству удовлетворяет значение 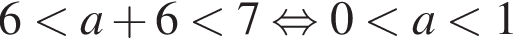 — неравенство верно;
— неравенство верно;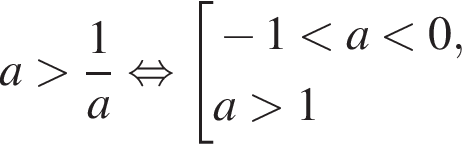 — неравенство неверно;
— неравенство неверно;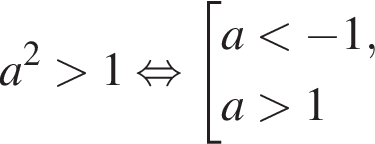 — неравенство неверно;
— неравенство неверно;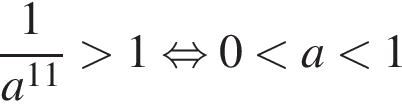 — неравенство верно;
— неравенство верно;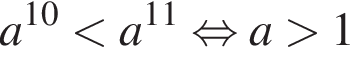 — неравенство неверно.
— неравенство неверно. Если бы Витя купил тетрадь в другом магазине, то было бы верно равенство
Если бы Витя купил тетрадь в другом магазине, то было бы верно равенство 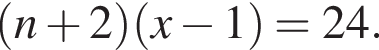 Решим систему уравнений:
Решим систему уравнений: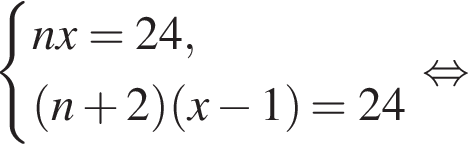
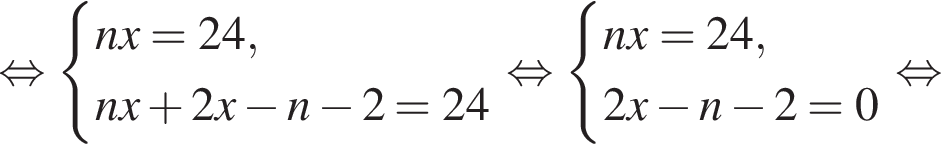
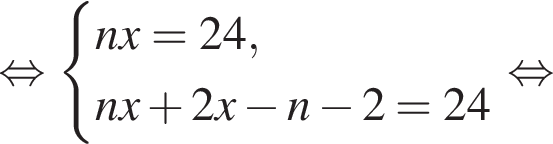
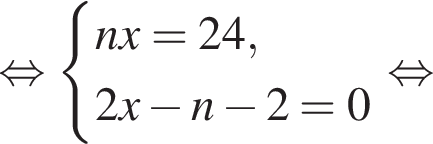
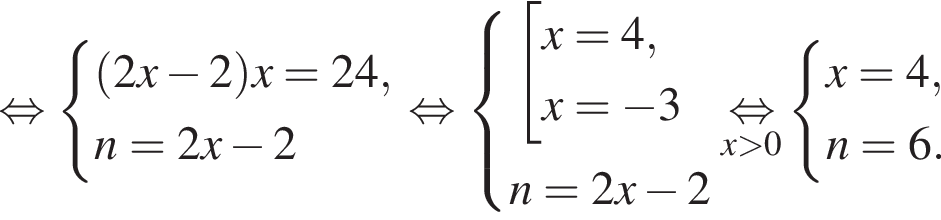
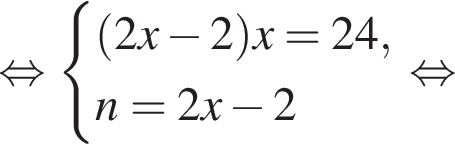
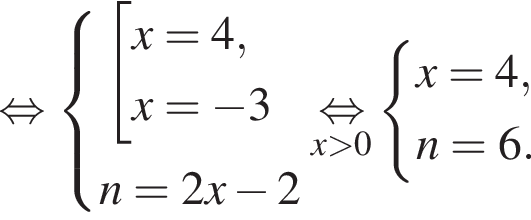
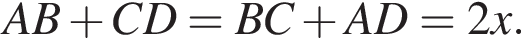 Сумма углов в равнобедренной трапеции, прилежащих к одной стороне равна 180°, откуда следует, что сумма углов, данная в условии — есть сумма углов при основании AD, которые равны.
Сумма углов в равнобедренной трапеции, прилежащих к одной стороне равна 180°, откуда следует, что сумма углов, данная в условии — есть сумма углов при основании AD, которые равны. 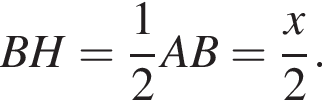 Поэтому из площади трапеции найдем x:
Поэтому из площади трапеции найдем x: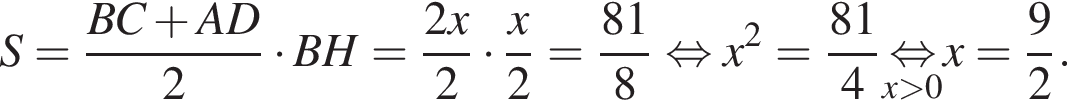
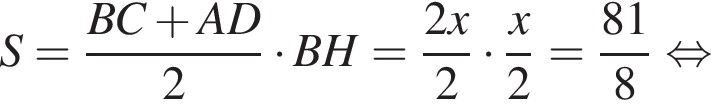
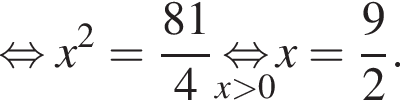
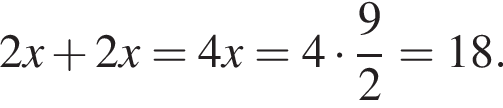
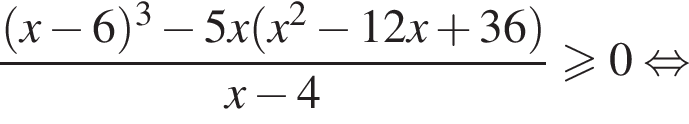
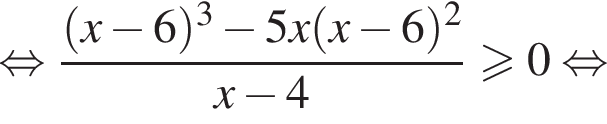
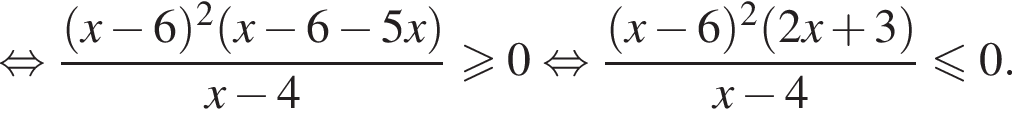
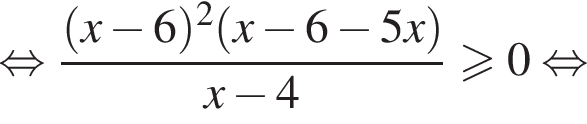
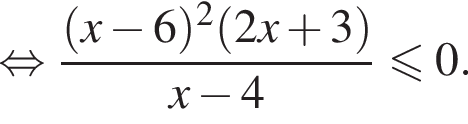
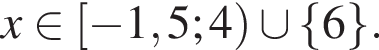 Целыми решениями неравенства являются числа −1, 0, 1, 2, 3, 6. Их сумма равна 11.
Целыми решениями неравенства являются числа −1, 0, 1, 2, 3, 6. Их сумма равна 11. Второе утверждение верно.
Второе утверждение верно.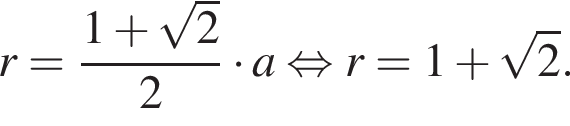
 где
где  — площадь равнобедренного треугольниками с боковыми сторонами, равными R и с основанием a.
— площадь равнобедренного треугольниками с боковыми сторонами, равными R и с основанием a.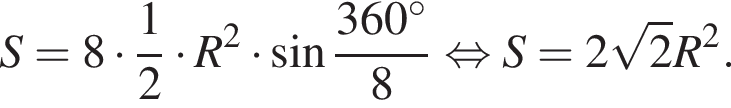
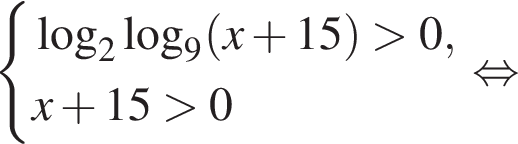
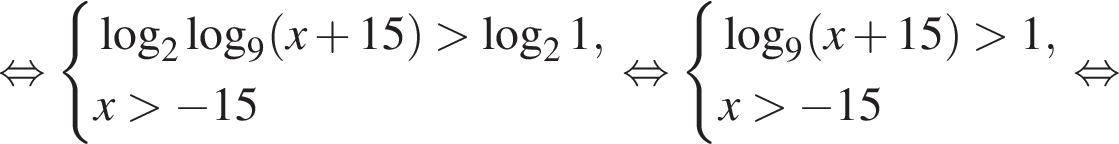
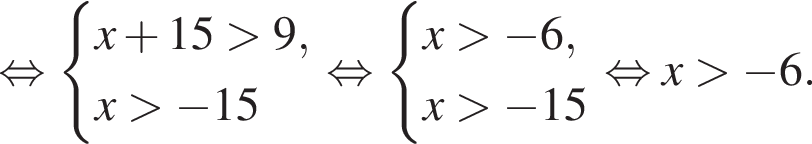
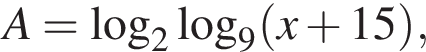 тогда:
тогда: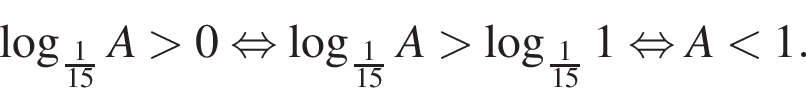
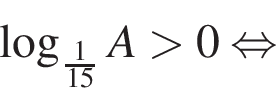
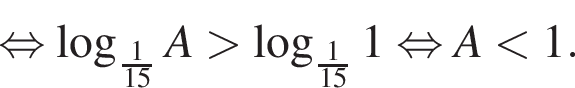

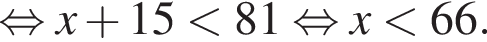


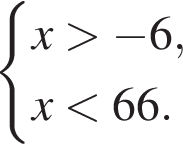 Поэтому наибольшее целое значение — 65, наименьшее целое значение −5, их сумма равна 60.
Поэтому наибольшее целое значение — 65, наименьшее целое значение −5, их сумма равна 60.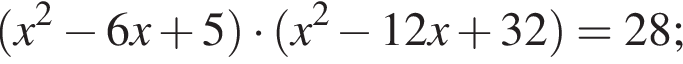


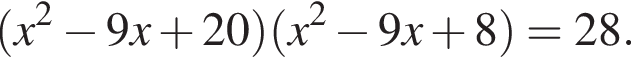
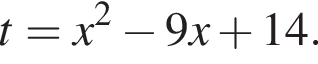 Получим:
Получим: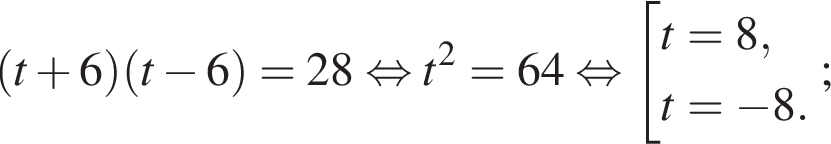
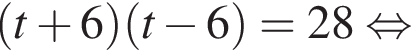
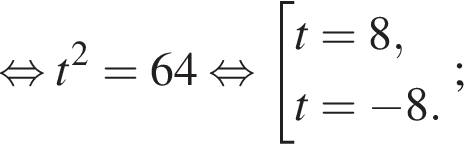
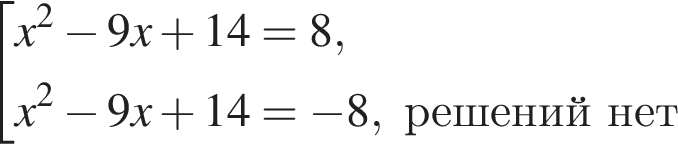
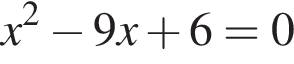 найдем по теореме Виета, она равна 9.
найдем по теореме Виета, она равна 9.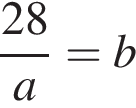 равносильно уравнению
равносильно уравнению  искать ОДЗ не требуется.
искать ОДЗ не требуется. Поскольку
Поскольку 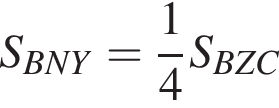 (NY — средняя линия), поэтому
(NY — средняя линия), поэтому 
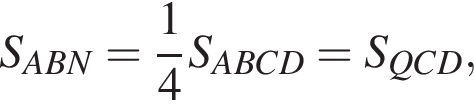 тогда
тогда 

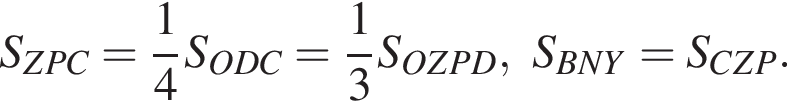
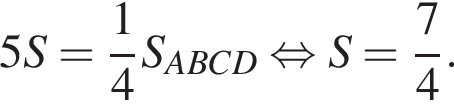
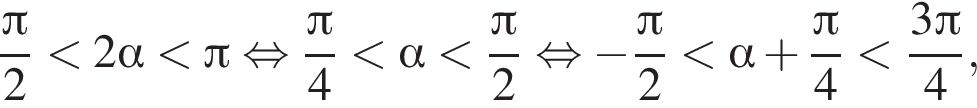

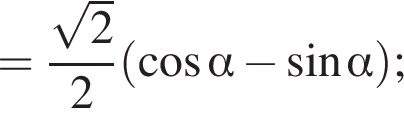
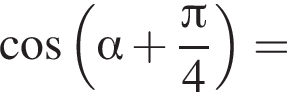
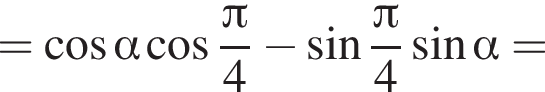
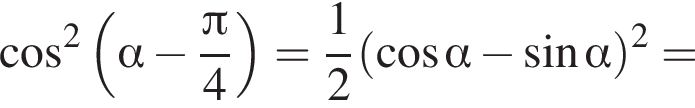

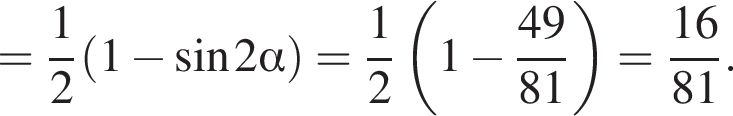
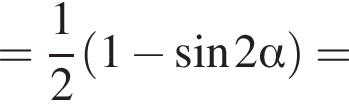
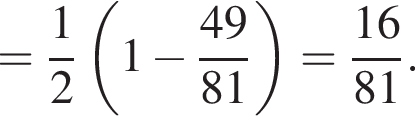
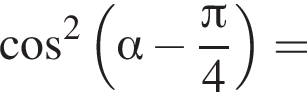
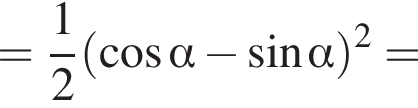
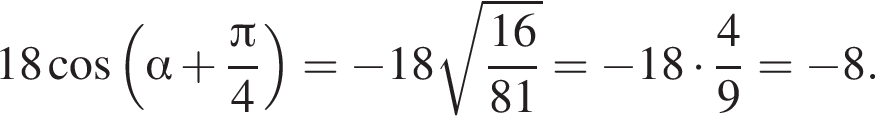
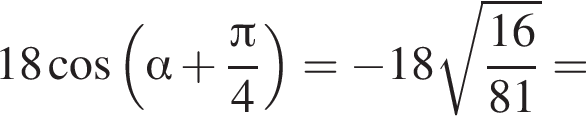
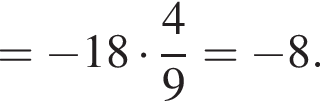
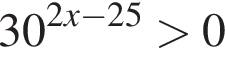 :
: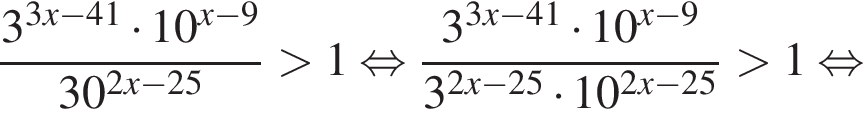
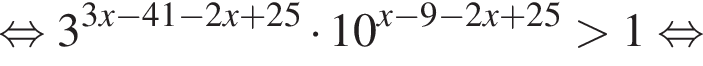
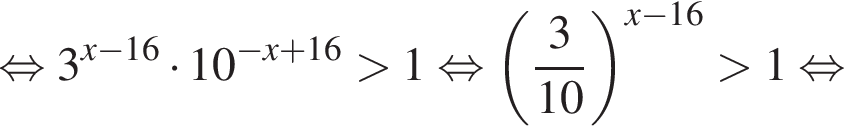
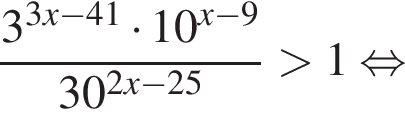
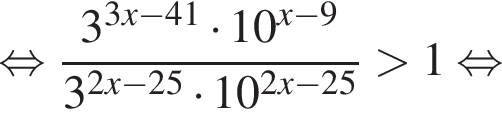
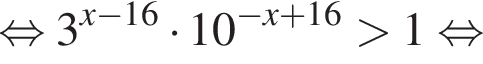
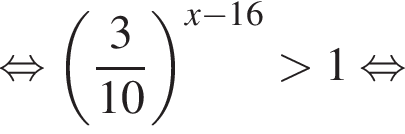
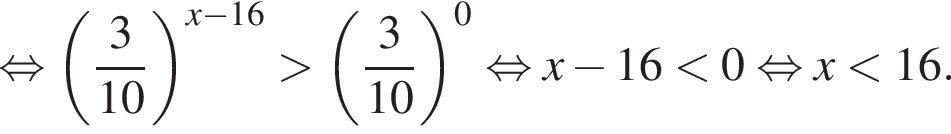
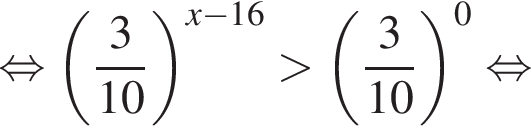
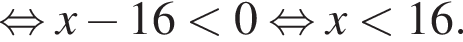
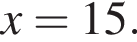

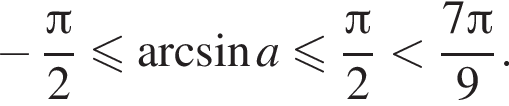
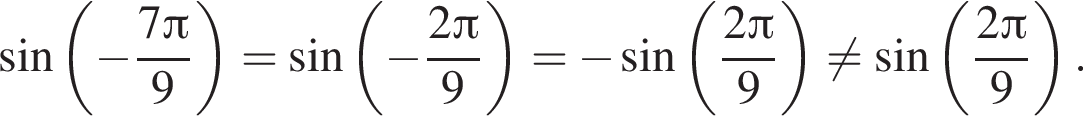
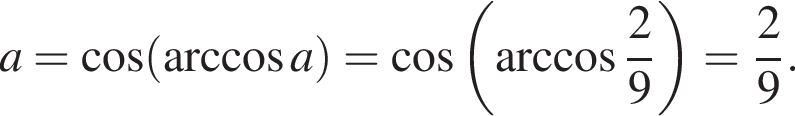
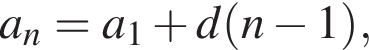 где d — разность арифметической прогрессии.
где d — разность арифметической прогрессии. 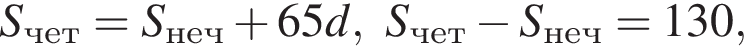 откуда
откуда 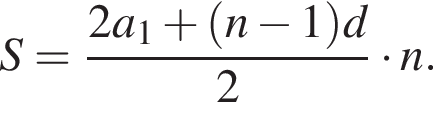 Следовательно, согласно условию, имеем:
Следовательно, согласно условию, имеем: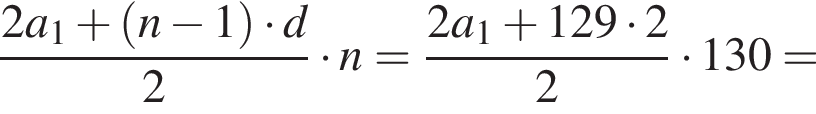
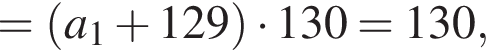
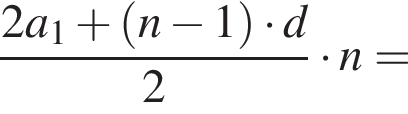
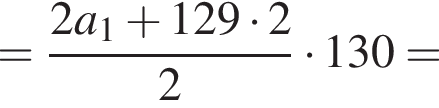
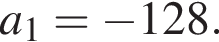 Получим
Получим 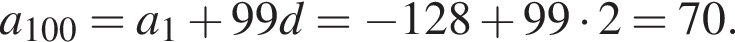
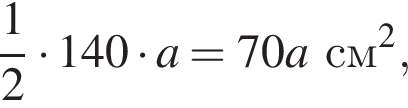 а расход краски равен
а расход краски равен 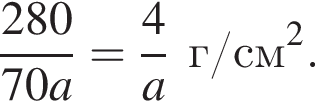 Площадь четырехугольной части листа равна
Площадь четырехугольной части листа равна 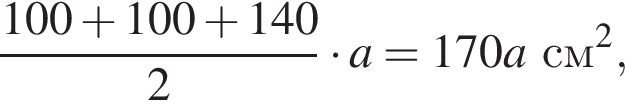
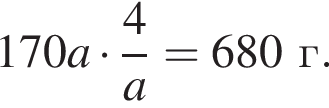
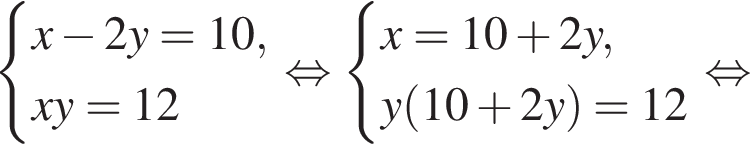
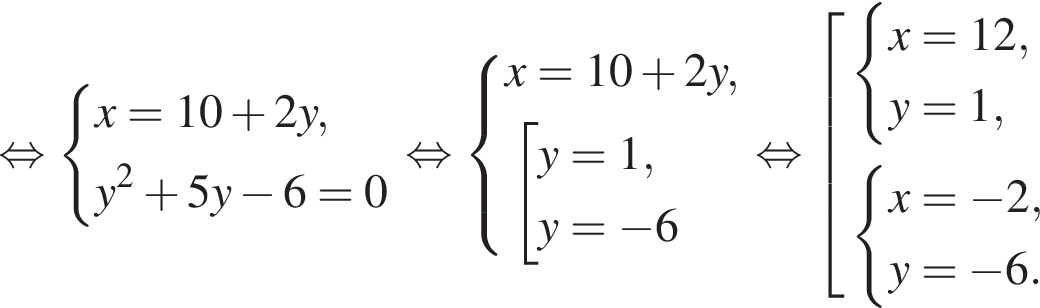
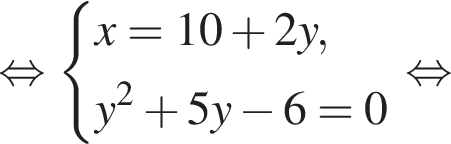
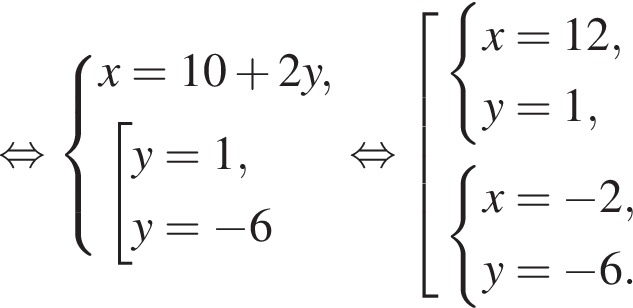
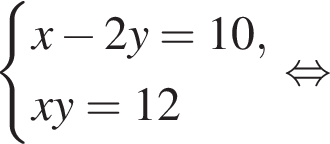
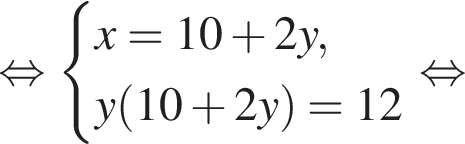
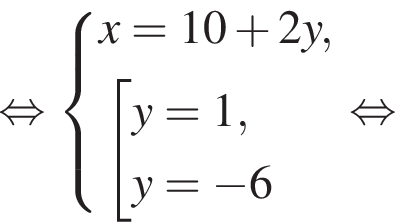
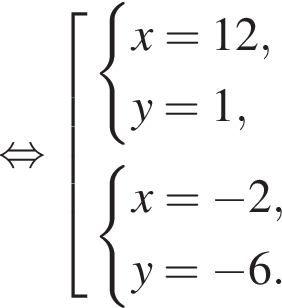
 равно
равно 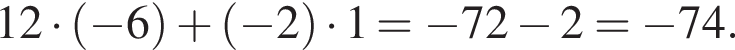
 Из соотношения
Из соотношения 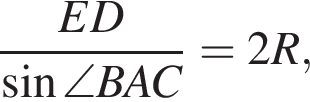
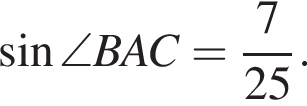
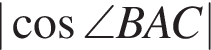 из основного тригонометрического тождества.
из основного тригонометрического тождества.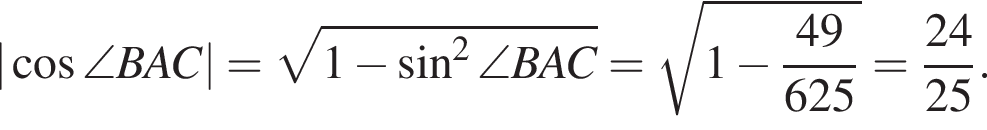
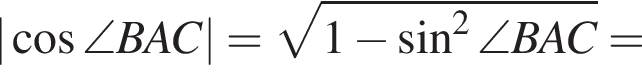
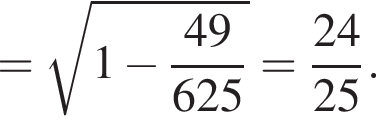
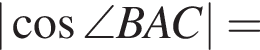
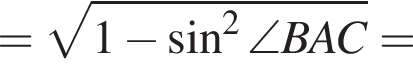
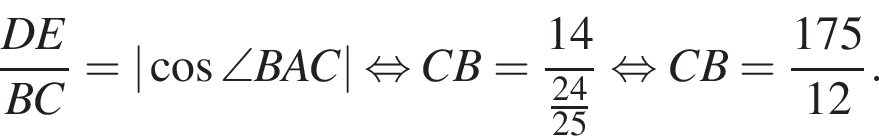
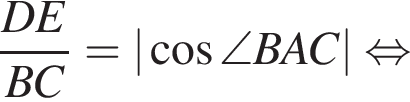
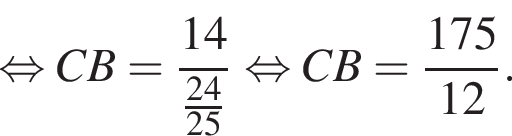
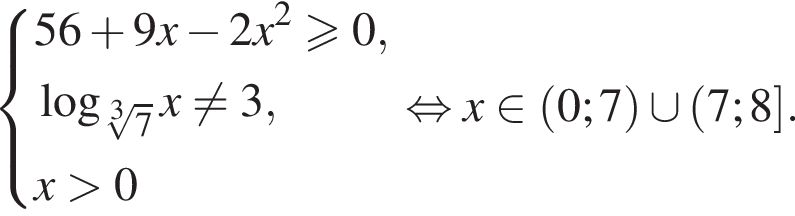
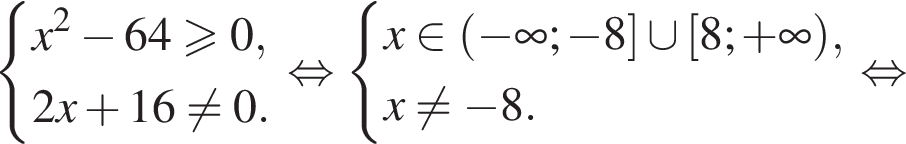
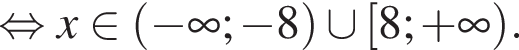
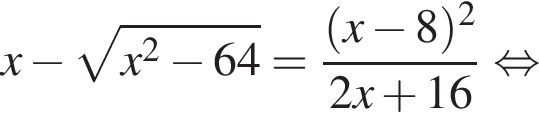
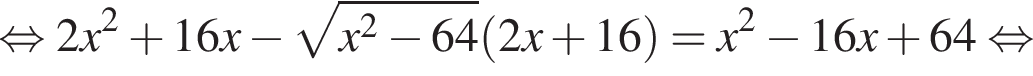
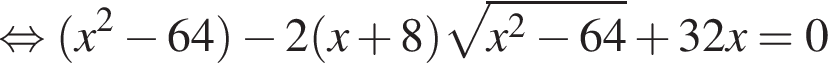
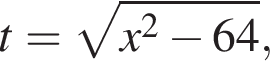 тогда
тогда 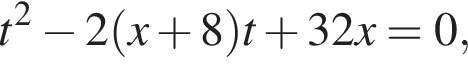 откуда
откуда 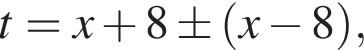 то есть
то есть